original link: https://www.douban.com/note/475843767/
What are some things that mathematics students know, but others don’t?
A股不开市,今天又无聊了。。。。所以转一个Quora的回答by Bhaskar Vashishth
I was waiting that someone will ask it. Was sick of same question about computer guys, and programmers.
Let me tell you some-
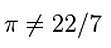
pi不等于7分之22
2. 0.999999…….=1
3. The Largest known prime number til this date is 2^{57885161}-1 . It has 17,425,170 digits. It is a Mersenne prime. 现在已知的最大的质数是2的57885161次方减1,它有1千7百42万5千1百70位数字,它是一个梅森素数。
4. ‘Balls’ can be square too.“球”可以是方形的。

额,这个说的是一个metric space里面,两个点(a1,b1) (a2,b2)的距离定义为|b1-a1|+|b2-a2|, 那么右边所示就是一个以(1,1)为中心、半径为3/4的open ball。就是一个正方形,四边的斜率分别是+1、-1。也就是说这个ball(square)里面的所有点到(1,1)的距离都不超过3/4。(这个有关基础拓扑。。。
5. Everything you can do with ruler and compass, you can do with compass alone. For more info read this- Geometric construction with the compass alone 所有可以尺规作图的,你都可以单独用圆规做到。(这个我也不懂。。。orz
6. The most famous theorem of mathematics- Pythagorean theorem- whose NCERT proof troubles school kids most, has more than 500 proofs, may be more than 1000’s. Eli Maor wrote a book in which he showed 367 proofs that were distinct enough to bother writing about separately. " (The Pythagorean Theorem)" 最有名的数学定理是勾股定理,而且让学森们头疼的是有超过500种甚至1000种证明方法。有个叫Eli Maor的人写了一本书写了367种证明方法。。。。(有够无聊的= =
7. Yes, 1>0 needs a proof. 嗯哼,1大于0是需要证明的。(挖鼻
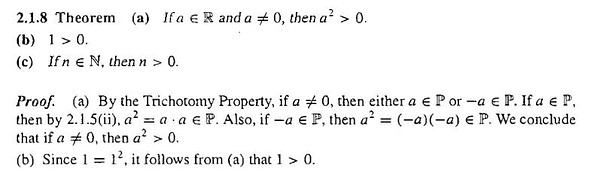
8. 0 can be equal to 2 , if you work in field of characterstic 2 i.e. \mathbb{Z}_2 . 0是可以等于2的,如果你是在特征为2的域里面。(这个是抽象代数,前段时间自学也没搞清楚)
9. Jordan Curve Theorem- It is a very tough theorem to prove that every simple closed curve divides a region into two parts, “interior” and “exterior”. 若尔当曲线定理-一个很难证明的定理,说的是任何一个简单的封闭曲线可以把一块地方分成两部分,“内部”和“外部”。
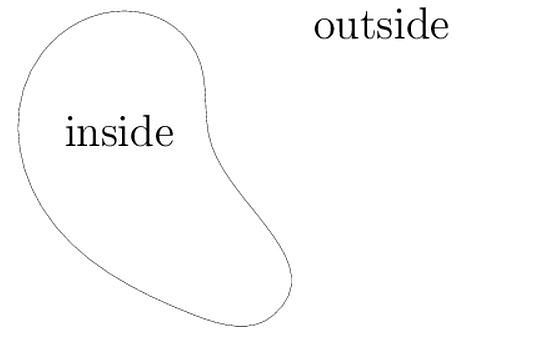
这个也是拓扑
10. A mathematician Kurt Godel has actually proved that God exist!! 有个数学家叫Kurt Godel证明出了上帝的确存在。。。。。(谢谢我看不懂。。。 The Proof-
11. A shape with finite volume must have finite surface area- False Gabriel’s Horn is an example. 一个有着有限体积的图形必然有着有限的表面积。-错的! (这个和极限limit相关吧)

托里拆利小号,体积是finite,但表面积是infinite
12. There are more rational numbers than there are integers- False 有理数比整数多-错的!其实两者是same size! 可参考这个答案
13. i^i is real number. i的i次方是个实数。 因为exp(i*Pi/2) = cos(Pi/2) + i*sin(Pi/2) = i,两边一起i次方,左边就是exp(-Pi/2)=0.20788,右边就是i^i。

有些数学定理吧,你知道它一定是对的,但是永远无法证明出来[doge]
15. The Fibonacci sequence is encoded in the number 1/89- ( 1/89 = 0.01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + 0.000000021 + 0.0000000034 …) 斐波那契数列(0,1,1,2,3,5,8,13…….)是这么编码的。。。。(我也不懂这个。。。)
16. Too much beauty in one pic..
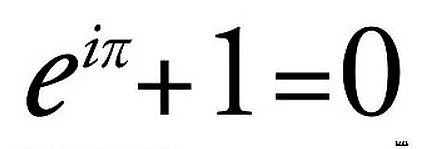
exp(i*Pi) = cos(Pi) + i*sin(Pi) = -1
17. 1+1/2+1/4+1/8+………. =2 Joke based on this- Infinitely many mathematicians walk into a bar. The first says, “I’ll have a beer.” The second says, “I’ll have half a beer.” The third says, “I’ll have a quarter of a beer.” The barman pulls out just two beers. The mathematicians are all like, “That’s all you’re giving us? How drunk do you expect us to get on that?” The bartender says, “Come on guys. Know your limits. 这个Joke就是几个数学家去酒吧喝酒被嘲笑了XDD。Know your limits
18. 1+1/2+1/3+1/4+………. =infinity Joke base on this- An infinite number of mathematicians walk into a bar. The first one orders a beer. The second orders half a beer. The third orders a third of a beer. The bartender bellows, “Get the hell out of here, are you trying to ruin me?” 这个也是很有名的Harmonic series,中文叫调和级数,它是divergent的,没有limit。
19. A pizza that has radius “z” and height “a” has volume Pi × z × z × a. 就是把Pizza当成一个圆柱体啦。。。
20. If you shuffle a pack of cards properly, chances are that exact order has never been seen before in the whole history of the universe. 洗牌之后的顺序极有可能是整个历史中都从未见过的。因为52的阶乘是非常大非常大的一个数。 Explanation - A deck of 52 cards can be ordered in 52! = 52*51*50*…*2*1 ways. But 52! is a very large number: larger than 8*10^{67} . How big is this number? Well, someone shuffling a deck of cards once per second since the beginning of the universe (believed to be about 14 billion years ago) would not have shuffled the deck more than 10^{18} times. 如果一个人从宇宙的开端(大约140亿年前)开始一秒钟洗一次牌,到现在为止洗牌的次数也不超过10的18次方。
21. Zero is even number. 零是偶数,这个很多人都知道吧。。。
Three Interesting Theorems- 22. The four-color theorem states that any map in a plane can be colored using four-colors in such a way that regions sharing a common boundary (other than a single point) do not share the same color. 四色定理:每个地图都可以用不多于四种颜色来染色,而且不会有两个邻接的区域颜色相同。(抄wiki的)
23. Brouwer’s Fixed Point Theorem (implication) says that if you take two sheets of paper, one lying directly above the other. If you crumple the top sheet (do not rip or tear the sheet), and place it on top of the other sheet, then there must be at least one point on the top sheet that is directly above the corresponding point on the bottom sheet! Do you believe that? 布劳威尔不动点定理:这里是一个比喻,说是两张纸,把一张纸弄皱放在另外一张纸上面,那么上面那张纸上至少有一个点是正好在下面那张纸上对应的一点的上方。(中文说不清楚,如果你懂不动点的意思是f(Xo)=Xo。)
24. Hairy Ball Theorem (Real life implication) - It states that given a ball with hairs all over it, it is impossible to comb the hairs continuously and have all the hairs lay flat. Some hair must be sticking straight up! 毛球定理 - 这个比喻是说如果一个毛球,是不可能连续性的将所有毛给梳平的,肯定会有毛仍然保持坚挺。XDDD

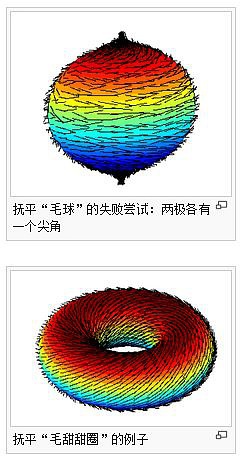
wiki上的图其实萌萌的呢毛甜甜圈w
25. It took Russell and Whitehead several hundred pages to prove that 1+1=2 in Principia Mathematica. Russell and Whitehead用几百页证明了1+1=2。
26. Divisibility by 7- Remove the last digit, double it, subtract it from the truncated original number and if the result is a multiple of seven, then so is the original number, keep repeating till number is small enough. 被7整除的特征: eg:1603 -> 160-2*3=154 -> 15-2*4=7, so 1603 is divisible by 7。
27. Random walk theory- A result by Polya states that in one or two dimension, a random walker returns to the origin infinitely many times but only a finite number of times in dimension 3 (or greater). Thus they say- “A drunk ant or a drunk man will always reach home but a drunk bird might not! 随机游走理论:一维和二维中,随机游走可以回到原点无数次,但是在三维或更高维中,只会回到原点有限次。 这个是随机过程(Stochastic Process)里的,股票也被认为是random walk,所以是无法预测的。
Mathematician exclusive jokes- 以下是一些数学相关joke,可以装逼,但是基本上觉得大部分人听不懂啊orz 而且已经有点离题。
28. “The B in Benoît B. Mandelbrot stand for Benoît B. Mandelbrot.” (If you know a little about Fractals) 这个我完全不懂,如果你懂分形。。。。。。
29. My Favourite- “A comathematician is a device for turning cotheorems into ffee.” (Hint look up Paul Erdos quotes). 保罗·爱多士是个很有名的数学家,因为他的高产,包括与人合作的论文,一共有1525篇论文发表,为现时发表论文数最多的数学家。有一个Erdős number(埃尔德什数),是描述数学论文中一个作者与埃尔德什的“合作距离”的一种方式。和六度分隔理论有关。 话说我查到的这句quote是A mathematician is a device for turning coffee into theorems。
30. “I went to visit him while he was lying ill at the hospital. I had come in taxi cab number 14 and remarked that it was a rather dull number. “No” he replied, “it is a very interesting number. It’s the smallest number expressible as the product of 7 and 2 in two different ways.”- Hint- Ramanujan’s most famous story. 这个我查过wiki之后看到的是1729,称为的士数Taxicab(n),定义为最小的数能以n个不同的方法表示成两个正立方数之和。1729=1^3+12^3=9^3+10^3。到现在为止也只找到6个Taxicab。
31. Prof: “Give an example of a vector space.” Student: “V” 有点冷。教授:给一个向量空间的例子。学生:V。
32. Why did the mathematician name his dog “Cauchy”? Because he left a residue at every pole. :P 为什么一个数学家把他的狗叫“Cauchy”?因为它会在每一个洞里留下点东西。。。。。。
以下不太懂= = 33. The primary reason Bourbaki stopped writing books was the realization that Lang was one single person. 34. “Let epsilon<0.” 35.
May be I will add more later. Thanks!